ACADEMIC DIRECTOR | AD
“Economics is a social science that seeks to explain human behavior, where one’s decisions can subconsciously affect the decisions of another.”
The theories that you learn in Mr. Edison’s class can play an essential role in your career if applied correctly, improving your decision-making in the future.
A brief insight into the world of economics.
A good example would be the theory of Price Elasticity Demand (PED). PED explains why fast food companies tend to reduce the portions of their food to save costs instead of increasing the prices, this is because they know their product is ‘price elastic’. If they were to increase the price of their food, consumers may prefer the lower prices of other fast food companies.
The power of understanding
Memorizing is short-term, understanding is long-term. Mr. Edison emphasizes on understanding rather than memorizing as he believes economics is a storybook written by researchers that reflects the reality.
Do you ever memorize a storybook? – NO.
Yet, you still able to tell the entire story to your child.
Teaching characteristic & Special note
- Cheat sheet allows students to recall and link the details in the chapter in a glance
- Powerful Mindmap that shows the connection of every theory in the chapter
- The “Whatapps support” that help to solve student’s curiosity and problem.
- Understand the personality of the student and tailor a teaching method for him/her.
Qualification
Degree
- Bachelor of Economics (Hons) in Financial Economics
Teaching experience & Education Skills
- More than 7 years of teaching experience
- Unique techniques in answering exam questions
- Prioritises interaction with students
- Allocates extra time for QnA sessions





Step by step guidance is crucial in effective learning process.
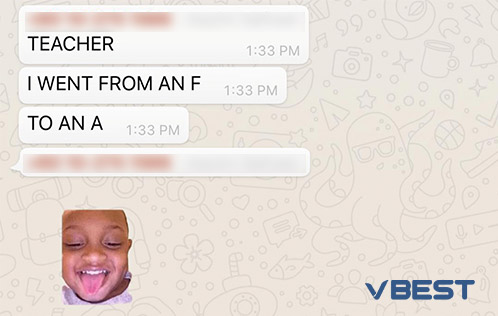
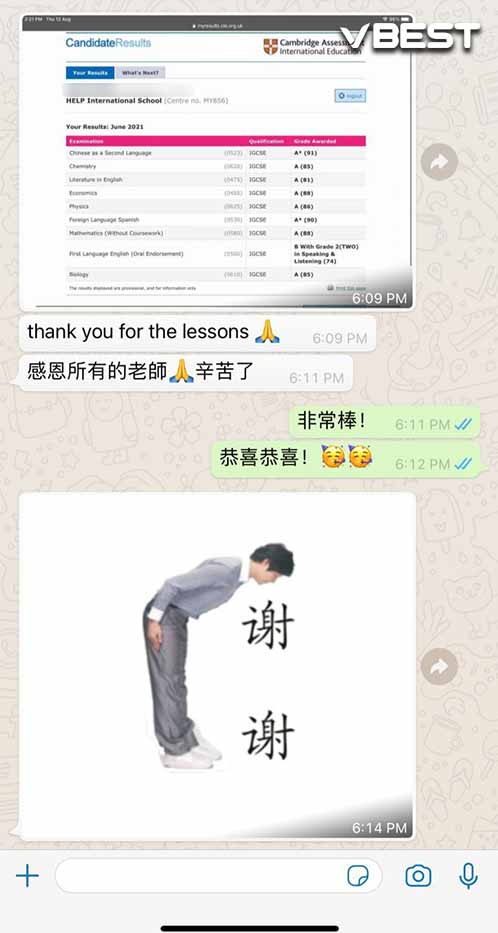
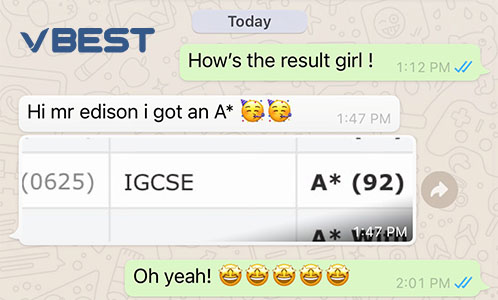
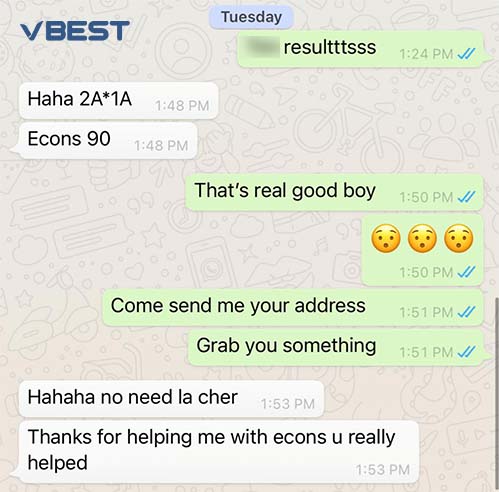
Students Outstanding Results
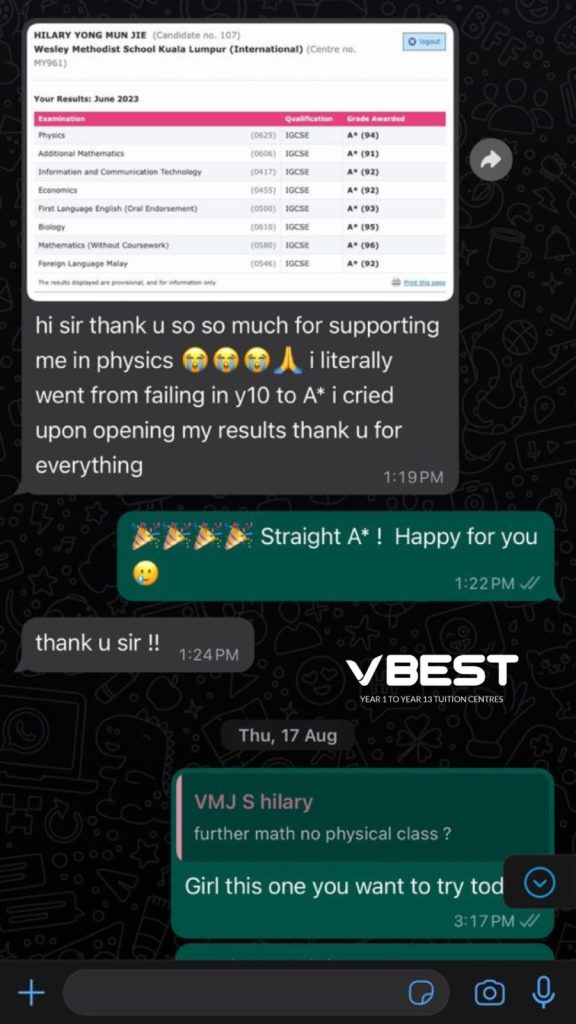
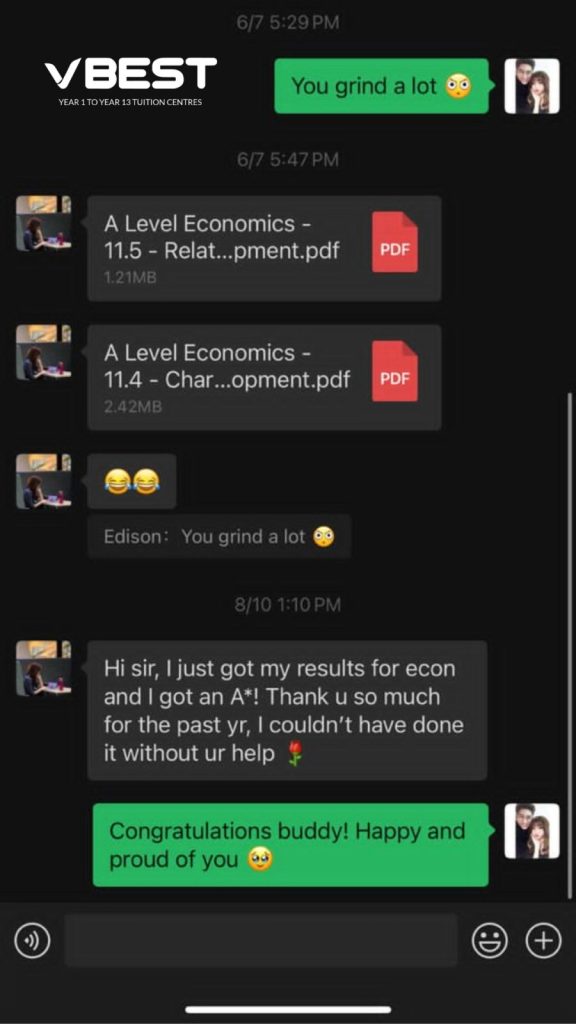
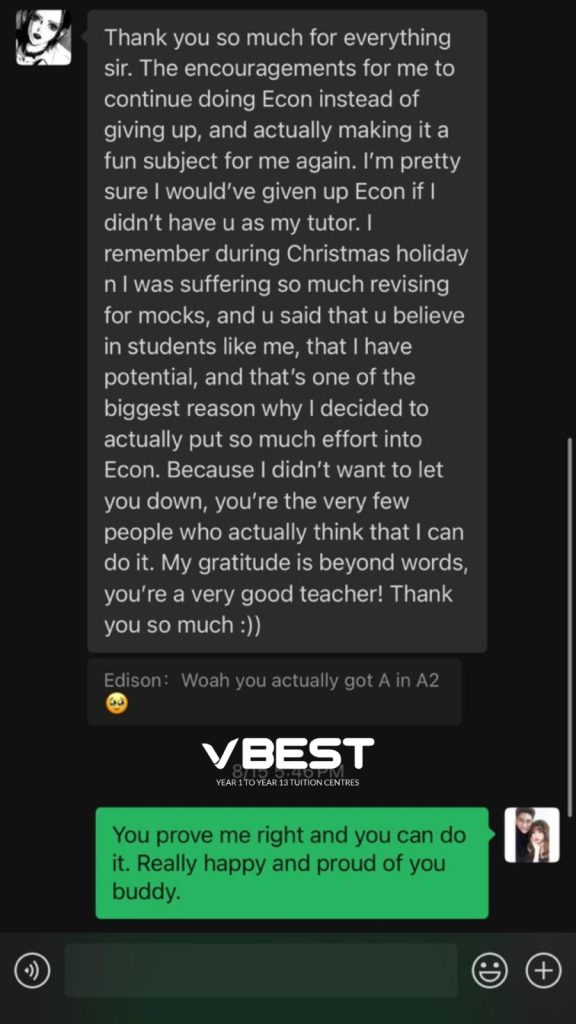
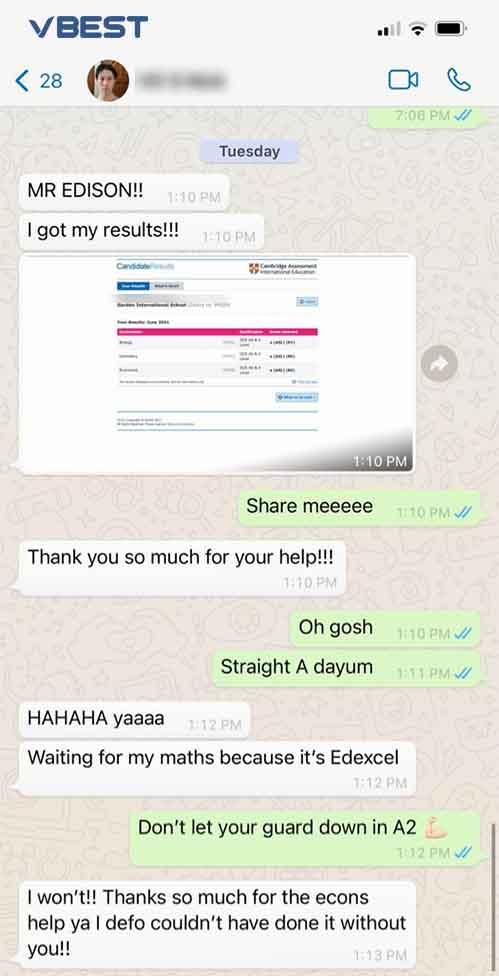
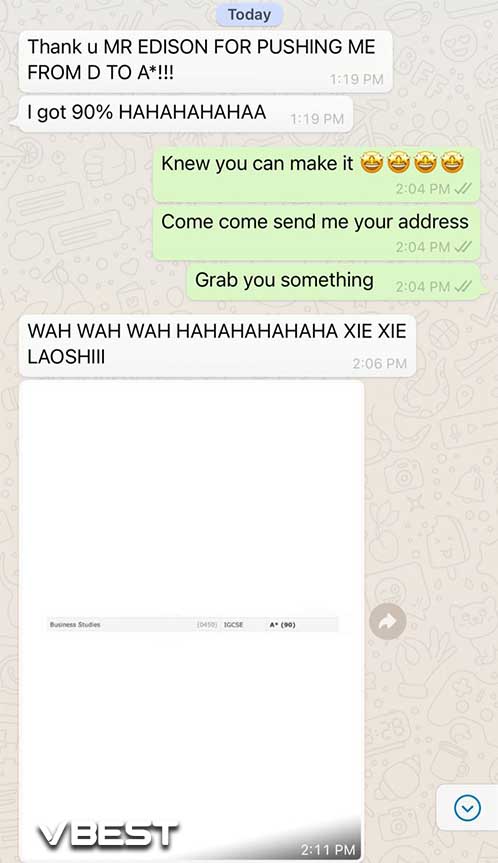
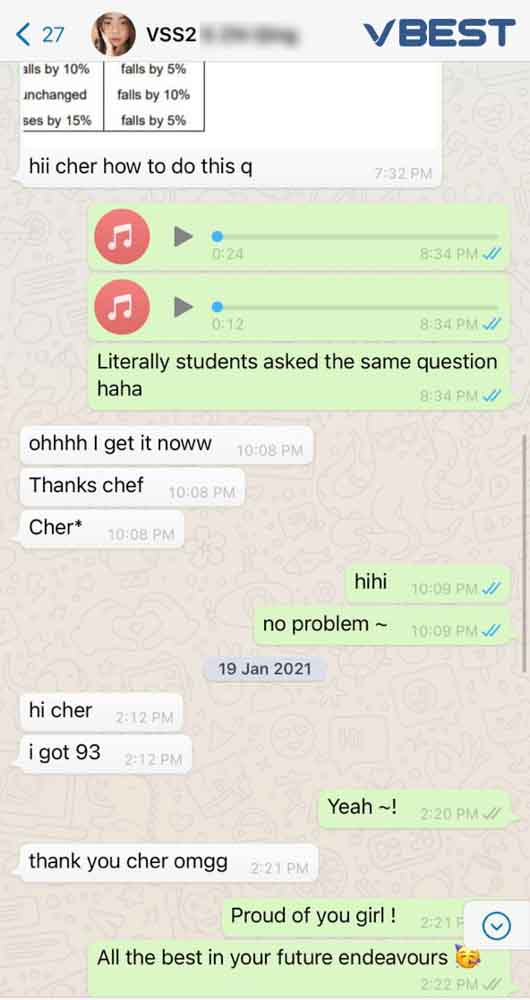
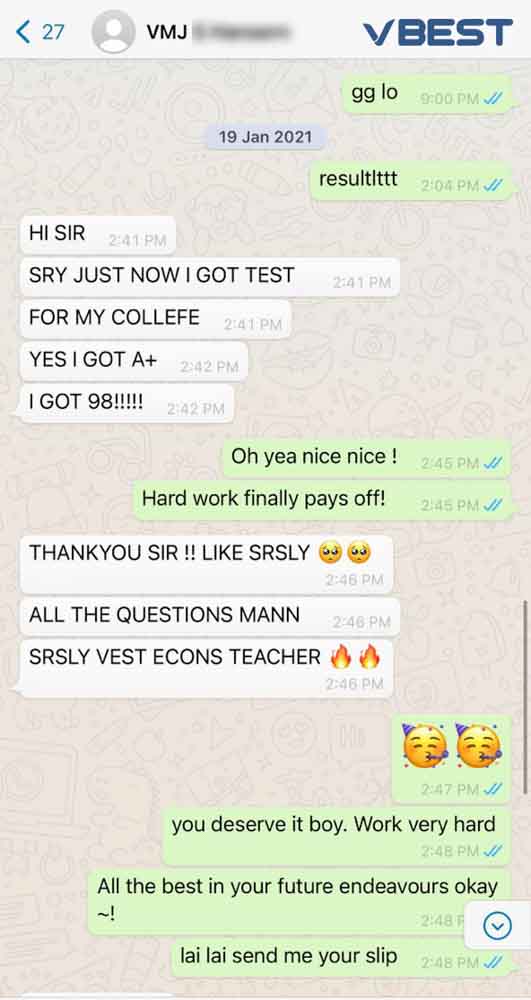
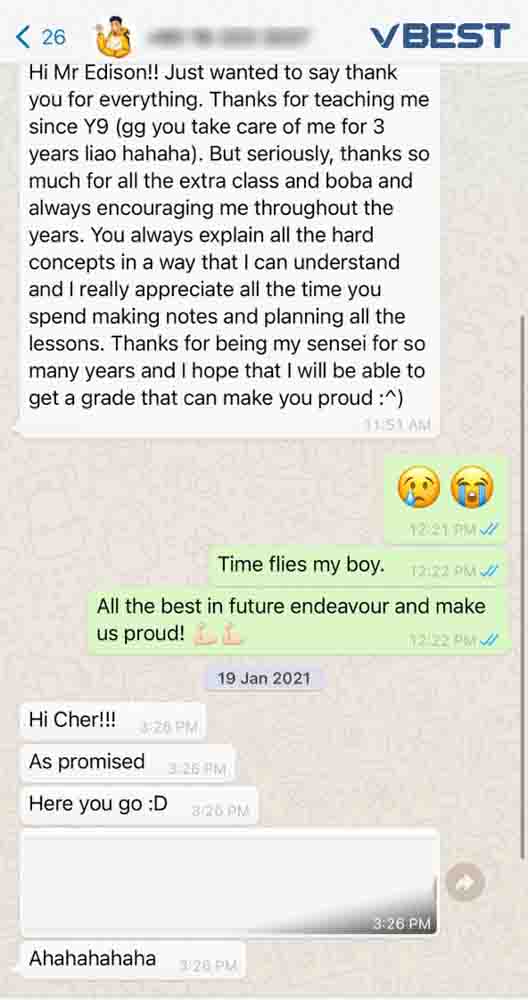
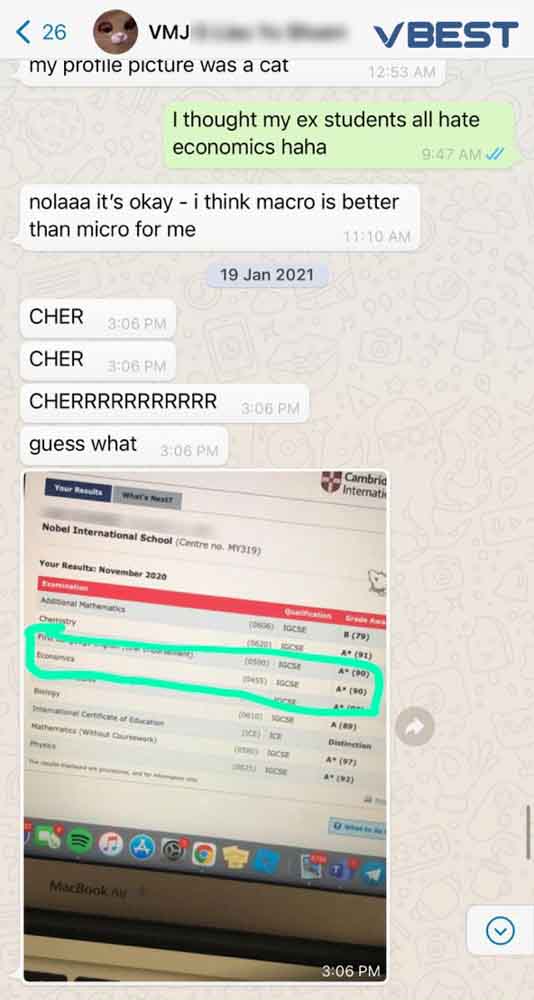
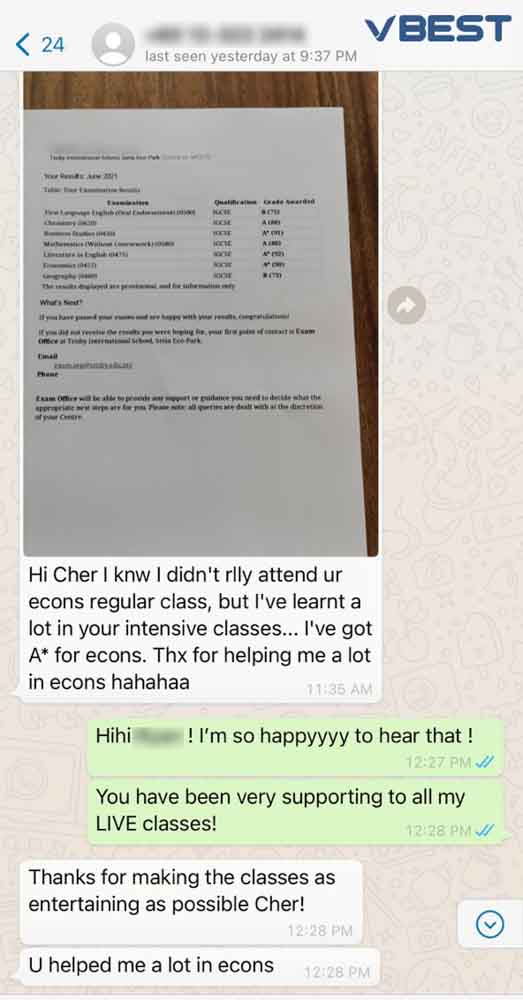
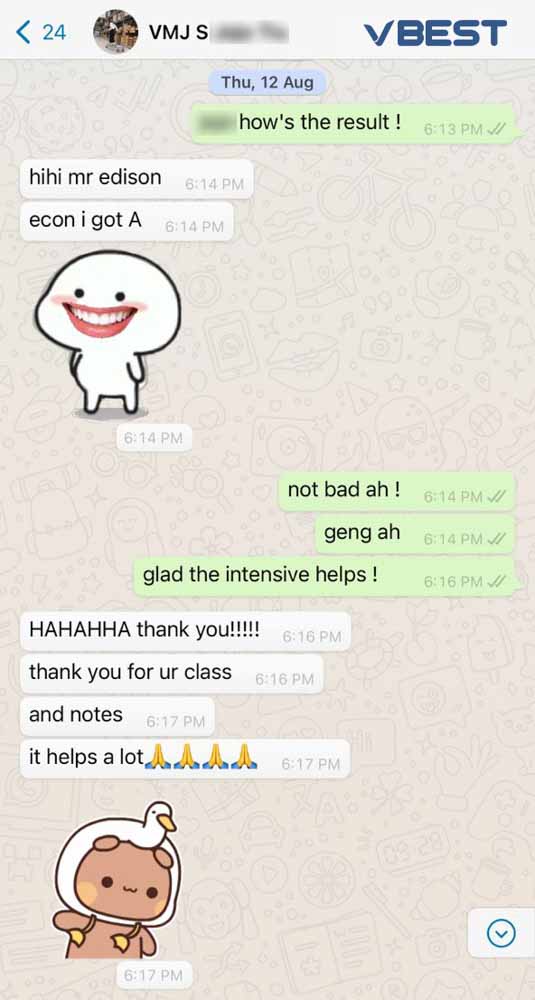
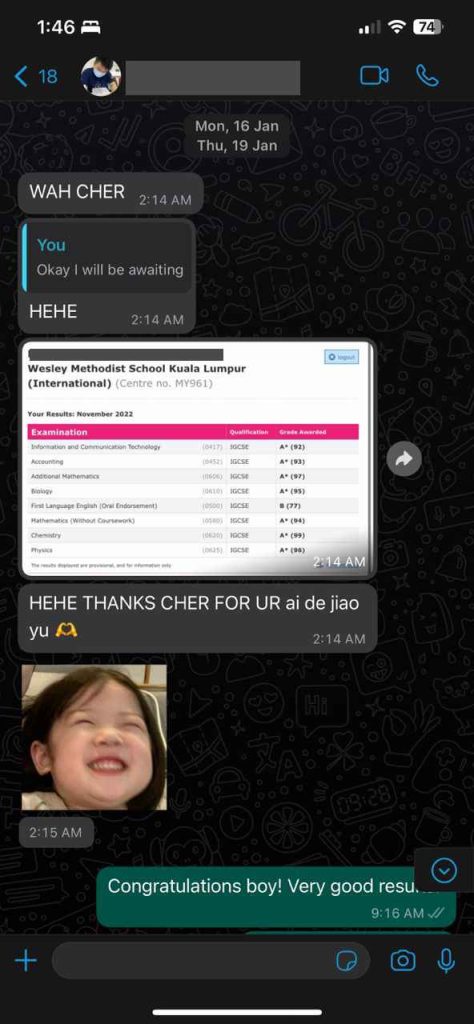
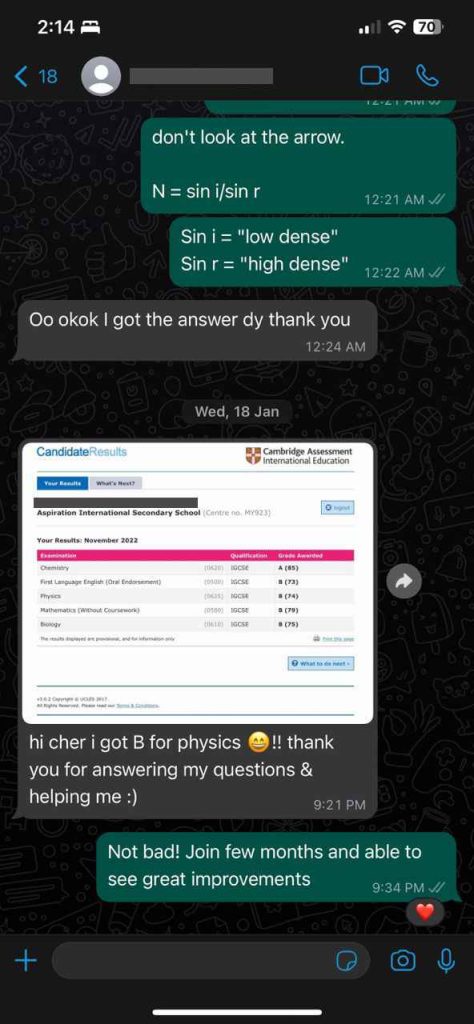
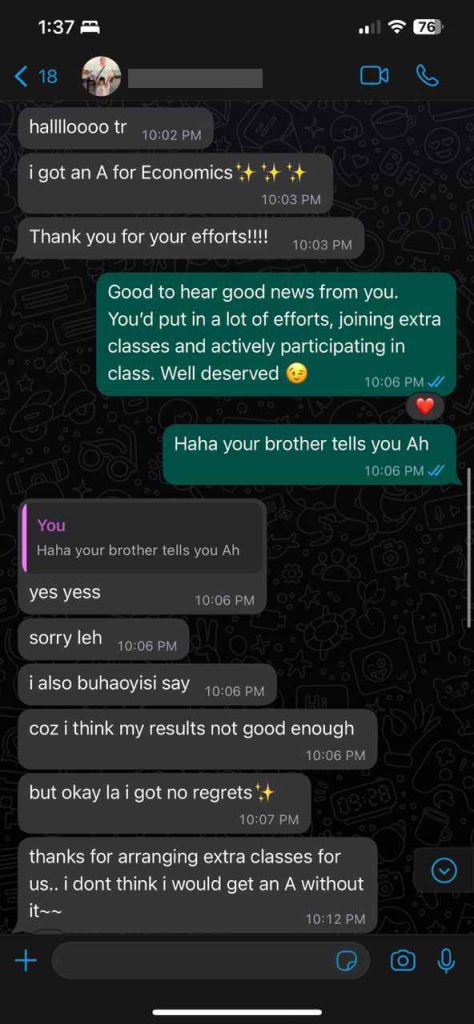
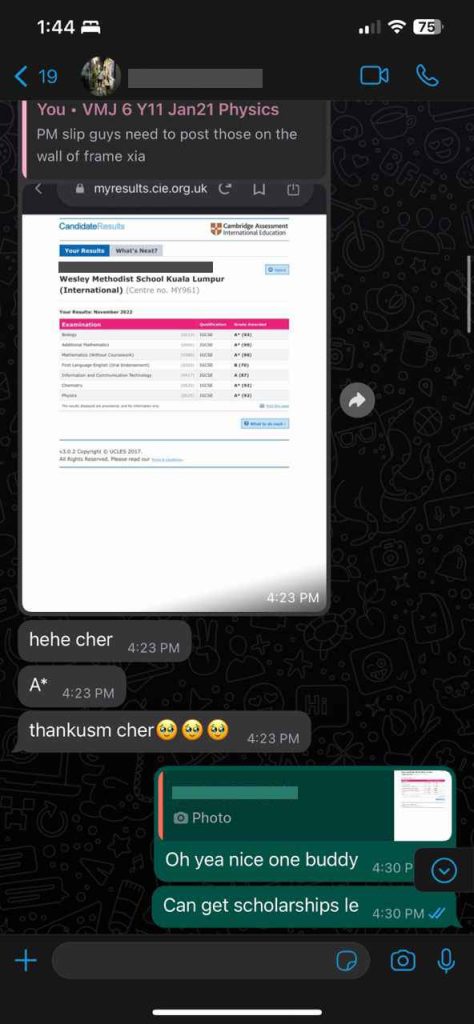
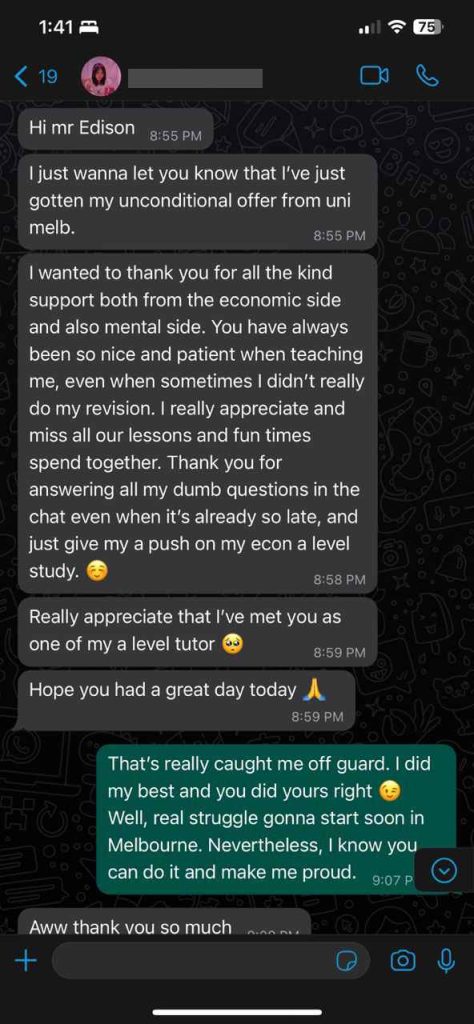
IGCSE
Economics
Alden Ong – Wesley Methodist – 91 A* – O/N 2020
Ameera – Beaconhouse International – 89 A – O/N 2020
Ashimita – Nobel – 87 A – O/N 2020
Shaun – Nobel – 80 A – O/N 2020
Qian Yun – Nobel – 91 A* – O/N 2020
Shie Wei – Beaconhouse International – 94 A* – O/N 2020
Zhi Qing – Wesley Methodist – 93 A* – O/N 2020
Claire – Wesley Methodist – 86 A – O/N 2020
Jayden – Wesley Methodist – 80 A – O/N 2020
Sue Jing – Wesley Methodist – 92 A* – O/N 2020
Liau Yu Shuen – Nobel – 90 A* – O/N 2020
Amber – Wesley Methodist – 97 A* – O/N 2020
Hanson Siah – Wesley Methodist – 98 A* – O/N 2020
Chally – Sri Emas – 85 A – O/N 2020
AS Level Economics
Nick – GIS – 85 A – M/J 2021
Zi Yun Zhang – GIS – 86 A – M/J 2021
Daniel Gam – HELP – 94 A* – M/J 2021
Chloe Chow – HELP – 93 A* – M/J 2021
A2 Level Economics
Timothy Chan – MCKL – 90 A* – M/J 2021
Li Ann – Taylor – 92 A* – M/J 2021
Xiang Yin – MCKL – 91 A* – M/J 2021
Jackie Siew – TARUC – A* – O/N 2020
Faris – Taylor – A* – O/N 2020
Physics
Benjamin Tan – Harvest – 95 A* – O/N 2020
Jonathan Tan – Harvest – 90 A* – O/N 2020
Shie Wei – Beaconhouse International – 91 A* – M/J 2021
Ray – Beaconhouse International – 95 A* – O/N 2020
Ryan – Beaconhouse International – 96 A* – O/N 2020
Elly – Beaconhouse International – 90 A* – O/N 2020
Andreana – Beaconhouse International – 92 A* – O/N 2020
Feng Min – Beaconhouse International – 94 A* – O/N 2020
Kireina – HELP – 92 A* – M/J 2021
Chally – Sri Emas – 86 A – O/N 2020

